1.      Data Mining – интеллектуальный анализ данных: определение, жизненный цикл данных, общая характеристика процесса анализа. 1

2.      Data Mining – интеллектуальный анализ данных: решаемые задачи, типы выявляемых закономерностей и используемые технологии и алгоритмы. 2

3.      Типы данных и шкал. 3

4.      Качество данных и связанные проблемы.. 4

5.      Классификация данных. Постановка задачи. Варианты задания исходных данных. Практическое применение классификации. 5

6.      Построение матрицы близости в кластерном анализе. Меры сходства объектов и их соответствие свойствам метрик. 5

7.      Классификация методов кластер-анализа. 6

8.      Иерархические агломеративные и дивизимные процедуры. Построение дендограммы. Формула рекуррентного пересчета расстояния между кластерами. 7

9.      Иерархические дивизимные процедуры.  (см. выше) 8

10.         Итеративные методы кластер-анализа, основанные на понятии ядра. Параллельные и последовательные процедуры. 8

11.         Методы построения размытых кластеров. Нечеткий кластерный анализ. 8

12.         Использование теории графов в кластер-анализе. 9

13.         Методы поиска модальных значений плотности. 9

14.         Проверка качества разбиения совокупности данных на кластеры. 10

15.         Локальные и глобальные правила остановки. 11

16.         Дискриминантный анализ (ДА): основные понятия, допущения модели и их влияние на результат. Основные этапы   11

17.         Построение канонических дискриминантных функций. Интерпретация коэффициентов. 12

18.         Проверка значимости дискриминантных функций. Остаточная дискриминантная способность. 13

19.         Построение правила классификации. Использование классифицирующих функций в ДА. Матрица классификации. 13

20.         Построение правила классификации на основе расстояния Махаланобиса и апостериорной вероятности. 13

21.         Процедуры отбора оптимального состава дискриминантных переменных. 14

22.         Снижение размерности данных. Постановка задачи и методы решения. 14

23.         Модели и методы факторного анализа. 14

24.         Метод главных компонент. 15

25.         Фундаментальная теоpема в случае коppелиpуемых и некоррелируемых фактоpов. 15

26.         Классификация факторов и связи между отдельными видами факторов. 15

27.         Составляющие полной дисперсии переменной (общность, хаpактеpность, спецефичность, надежность). 15

28.         Схема решения и основные проблемы факторного анализа. 15

29.         Геометрическая интерпретация модели факторного анализа. 15

30.         Пространство общих факторов и полное фактоpное пpостpанство. 16

31.         Проблема факторов. Выделение факторов с помощью метода главных компонент. Другие методы решения  16

32.         Критерии оценки числа факторов, подлежащих выделению. 17

33.         Пpоблема общности. В чем она состоит и как pешается. 18

34.         Проблема вращения и понятие наипростейшей факторной структуры.. 18

35.         Цель и конечный pезультат оpтогонального вpащения. 18

36.         Методы и критерии в ортогональном вращении. 18

37.         Цель и конечный pезультат косоугольного вpащения. Первичное и вторичное факторное решение. Критерии и методы, применяемые в косоугольном вращении. 19

38.         Измерение факторов. 19

39.         Программное обеспечение, используемое для интеллектуального анализа данных. 19

40.         Методы визуализации многомерных  данных. 20

41.         Text Mining. 20

42.         Web Mining. 21

 

 

1.       Data Mining – интеллектуальный анализ данных: определение, жизненный цикл данных, общая характеристика процесса анализа

 

Data Mining

(«Добыча», «Раскопка данных»)

- это процесс, цель которого – обнаружить новые значимые корреляции, образцы и тенденции в результате просеивания большого объема хранимых данных с использованием методик распознавания образцов плюс [применение] статистических и математических методов.

- это исследование и обнаружение «машинными» методами (алгоритмами, средствами искусственного интеллекта) в сырых данных скрытых знаний, которые ранее не были известны. Нетривиальны, практически полезны, доступны для интерпретации человеком.

 

Жизненный цикл данных:

1.Источники данных: внутренние данные, внешние данные, личные данные;

2.Хранилища данных;

3.Витрины данных;

4.Анализ данных: OLAP, запросы, Data Mining;

5.Результат: визуализация данных, решения, менеджмент знаний;

6.Импорт в другие системы для обработки: CRM, ERP…

 

1.        Определение проблемы;

2.        Сбор данных;

3.        Выполнение первичной обработки данных;

4.        Запуск модели на выполнение;

5.        Интерпретация модели и выводы.

2.       Data Mining – интеллектуальный анализ данных: решаемые задачи, типы выявляемых закономерностей и используемые технологии и алгоритмы.

 

Задачи, решаемые Data Mining:

·         Классификация – отнесение входного вектора (объекта, события, наблюдения) к одному из заранее известных классов.

·         Кластеризация – разделение множества входных векторов на группы (кластеры) по степени «похожести» друг на друга.

·         Регрессия – установление зависимости непрерывными входным и выходным векторами.

·         Ассоциация – поиск повторяющихся паттернов. Например, поиск устойчивых связей в корзине покупателя (market basket analysis) – вместе с пивом покупают орешки.

·         Сокращение описания – для визуализации данных, лаконизма моделей, упрощения счета и интерпретации, сжатия объемов собираемой и хранимой информации.

·         Последовательные шаблоны – аналогично задаче ассоциации, но с учетом временной составляющей. Например, поиск причинно-следственных связей.

·         Прогнозирование – аналогично задаче регрессии, но с учетом временной составляющей. Например, прогноз трендов финансовых показателей.

·         Анализ отклонений – выявление наиболее нехарактерных паттернов. Например, выявление нетипичной сетевой активности позволяет обнаружить вредоносные программы.

 

В литературе можно встретить еще ряд классов задач. Базовыми задачами являются первые пять. Остальные задачи сводятся к ним тем или иным способом.

 

Типы выявляемых закономерностей:

·          Ассоциация – высокая вероятность связи событий друг с другом (например, один товар часто приобретается вместе с другим);

·          Последовательность – высокая вероятность цепочки связанных во времени событий (например, в течение определенного срока после приобретения одного товара будет с высокой степенью вероятности приобретен другой);

·          Классификация – имеются признаки, характеризующие группу, к которой принадлежит то или иное событие или объект (обычно при этом на основании анализа уже классифицированных событий формулируются некие правила);

·          Кластеризация – закономерность, сходная с классификацией и отличающаяся от нее тем, что сами группы при этом не заданы – они выявляются автоматически в процессе обработки данных;

·          Временные закономерности – наличие шаблонов в динамике поведения тех или иных данных (типичный пример – сезонные колебания спроса на те или иные товары, либо услуги), используемых для прогнозирования.

 

Используемые технологии и алгоритмы:

·          Регрессионный, дисперсионный и корреляционный анализ – реализован в большинстве современных статистических пакетов, в частности, в продуктах компаний SAS Institute, StatSoft и др.

·          Методы анализа, базирующиеся на эмпирических моделях – для анализа в конкретной предметной области и применяются в недорогих средствах финансового анализа.

·          Обнаружение аномалий/отклонений – определение серьезных отклонений от нормального поведения.

·          Кластерные модели  - применяются для объединения сходных событий в группы на основании сходных значений нескольких полей в наборе данных. Применяются различные алгоритмы группировки, например, метод «ближайшего соседа».

·          Деревья решений – иерархическая структура, базирующаяся на наборе вопросов, подразумевающих ответ «да» или «нет». Не способны находить «лучшие» правила в данных (наиболее полные и точные).

·          Алгоритмы ограниченного перебора – вычисляющие частоты комбинаций простых логических событий в подгруппах данных.

·          Нейросетевые алгоритмы – идея которых основана на аналогии с функционированием нервной ткани и заключается в том, что исходные параметры рассматриаются как сигналы, преобразующиеся в соответствии с имеющимися связями между «нейронами», а в качестве ответа, являющегося результатом анализа, рассматривается отклик всей сети на исходные данные.

·          Эволюционное программирование – поиск и генерация алгоритма, выражающего взаимозависимость данных, на основании изначально заданного алгоритма, модифицирующегося в процессе поиска.

·          Системы рассуждений на основе аналогичных случаев –не создают каких-либо моделей или правил, обобщающих предыдущий опыт, произвол при выборе меры близости.

·          Генетические алгоритмы – критерий отбора хромосом и используемые процедуры являются эвристическими и далеко не гарантируют «лучшего» решения.

 

3.       Типы данных и шкал.

 

Шкала – кортеж из трех элементов <x,ϕ,y>, где  x – реальный объект, ϕ – гомоморфное отображение X на Y, y – шкала; это правило, в соответствии с которым объектам присваиваются числа.

·          Номинальные – простейший вид измерений; качественная шкала (шкала наименований); цель – выявление различий между объектами разных классов, например, номера машин, телефонов, коды городов. То есть символы 1 и 2 в шкальных обозначениях являются не числами, а цифрами.

·          Ранговые (шкалы порядка) – шкала, у которой множество ϕ состоит из всех монотонно возрастающих допустимых преобразований шкальных значений. Допускает не только различие объектов, как номинальный тип, но используется и для упорядочения объектов по измеряемым свойствам (во времени, в пространстве, в соответсвии с каким-либо свойством объекта, которое не обязательно точно измерять или которое не может быть измерено). Например, шкалы силы ветра, силы землятресения, сортности товара и т.д.).

·          Интервальные – наиболее важная шкала; содержит шкалы, единственные с точностью до множества положительных линейных допустимых преобразований вида ϕ(x) = ax + b, а > 0, b – любое значение. Свойство – сохранение неизменных отношений интервалов в эквивалентных шкалах. При переходе к эквивалентным с помощью преобразований происходит изменение начала отсчета (параметр b) и масштаба измерений (параметр а). Сохраняют различие и упорядочивание измеряемых объектов, как и предыдущие. Пример, шкалы температур, время выполнения задания, любые временные и пространственные характеристики объектов.

·          Отношений (подобия) - шкала, у которой множество ϕ состоит из преобразований вида ϕ(x) = ax, а > 0. Свойство – сохранение неизменных отношений численных оценок объектов, то есть во сколько раз свойство одного объекта превосходит это же свойство другого объекта. Образуются из шкал интервалов фиксированием нулевого значения параметра  b: b=0. Переход от одной шкалы к другой осуществляется с помощью преобразования подобия. Пример, измерение массы в кг, футах и т.д.

·          Разностей – шкалы, единственные с точностью до преобразований сдвига    ϕ(x) = x + b; меняется только начало отсчета. Свойство – сохранений разностей численных оценок объектов. Образуются из шкал интервалов фиксированием нулевого значения параметра  а: а=1. Сохраняют отношения расстояний между парами объектов. Пример: измерение прироста продукции предприятий (в абсолютных значениях в текущем году по сравнению с прошлым и т.д.

·          Абсолютные – шкалы, в которых единственными допустимыми преобразованиями являются тождественные преобразования ϕ(x) = x. Частный случай всех других. Пример: измерения количества объектов, предметов, решений, событий и т.д.

·          Промежуточные – степенная ax^b, логарифмическая шкала.

·          Дихотомические – содержит только две категории, например, пол.

 

Типы данных:

·          Данные, состоящие из записей (Record) – представлены набором записей, каждая из которых содержит фиксированный набор атрибутов.

o    Data Matrix – представление данных в виде mxn матрицы, где m строк (строка – объект) и n столбцов (один столбец – атрибут).

o    Document Data – каждый документ описывается в виде ‘term’ вектора. Значение каждого компонента – множество вхождений соответствующего ‘term’ в документ.

o   

o    Transaction Data – особый тип данных в виде записей, где каждая запись (транзакция) включает набор значений, например, список покупок клиента.

·          Графические данные (Graph) – данные представлены в виде графа.

o    World Wide Web – интернет;

o    Molecular Structures – молекулярные структуры.

·          Упорядоченные данные (Ordered) – например, последовательность транзакций

o    Spatial Data – пространственные данные, например, географические;

o    Temporal Data – временные данные;

o    Sequential Data – последовательности данных;

o    Genetic Sequence Data – генетические последовательности данных.

 

4.       Качество данных и связанные проблемы.

 

Для обработки данных методами Data Mining необходимы качественные данные. Но в реальной жизни мы сталкиваемся с проблемами, связанными с качеством.

·          Шум – связан с модификацией оригинальных значений;

·          Выбросы – объекты данных с характеристиками, которые значительно отличаются от большинства объектов в наборе данных.

·          Пропущенные значения – связаны с тем, что не всегда могут быть получены данные, по причине нежелания предоставления данных, или отсутствия их. А также из-за ошибок ввода операторами. Способы обработки: исключение объектов из набора данных; вычисление пропущенных значений; игнорирование пропущ. значений в ходе анализа; замена на возможные значения (с указанием вероятности)

·          Дупликаты в данных – объекты в наборе данных, которые являются полными или неполными дупликатами друг друга. Например, один и тот же человек с разными мейлами. Чистка данных: процесс обработки дупликатов. Например, soundex.

(*посмотреть документацию на работе*)

 

5.       Классификация данных. Постановка задачи. Варианты задания исходных данных. Практическое применение классификации. 

 

Классификация – разделение рассматриваемой совокупности объектов или явлений на однородные, в определенном смысле, группы. При этом термин «классификация» используется как для самого процесса разделения, так и для результата.

 

Постановка задачи: формулировка задачи; формализация задачи. Включает также описание статического и динамического поведения исследуемых объектов.

 

Классификация может быть одномерной (по одному признаку) и многомерной (по двум и более признакам). Правила классификации: (1)в каждом акте деления необходимо применять только одно основание; (2) деление должно быть соразмерным, т.е. общий объем видовых понятий должен равняться объему делимого родового понятия; (3) члены деления должны взаимно исключать друг друга, их объемы не должны перекрещиваться; (4) деление должно быть последовательным.

Различают классификации: Естественную - по существенным признакам, характеризующим внутреннюю общность предметов и явлений. Искусственную - по внешнему признаку и служит для придания множеству объектов нужного порядка. Простой - деление родового понятия только по признаку и только один раз до раскрытия всех видов. Сложной - для деления одного понятия по разным основаниям и синтеза таких простых делений в единое целое. Задачей классификации часто называют предсказание категориальной зависимой переменной на основе выборки непрерывных и/или категориальных переменных.

 

Варианты задания исходных данных:

·          Матрица «объект-свойство» - где каждый элемент матрицы – это значение j-го признака у i-го объекта. То есть строка характеризует некоторый объект в наборе данных.

·          Матрица сходства – где каждый элемент матрицы характеризует сходство объектов Oi и Oj.

·          Запись

·          Документ

·          Транзакция

·          Граф

·          Последовательность

 

Практическое применение: ?

 

6.       Построение матрицы близости в кластерном анализе. Меры сходства объектов и их соответствие свойствам метрик.

 

Мера близости или сходства – это величина, имеющая предел и возрастающая с возрастанием близости объектов.

Условия для выбора меры близости: симметричность, различимость (aij<>1,если i <> j), тождественность (aii = 1).

·          Коэффициенты корреляции – самая распространенная мера сходства при иследованиях в области социальных наук. Наиболее известный – смешанный момент корреляции (К.Пирсон):

        X_ik – значение k-ой переменной для i-го объекта;

         - среднее значений всех переменных i-го объекта;

        P – число переменных.

 

«-» мера чувствительна к форме за счет снижения чувствительности к величине различий между переменными.

«-» корреляция, вычисленная этим способом, не имеет статистического смысла, поскольку среднее значение определяется по совокупности всевозможных разнотипных переменных для объекта, а не совокупности объектов.

 

·          Меры расстояния (несходства) – пользуются широкой популярностью. Обладают своствами: симметричности, неотрицательности, минимальное значение для двух идентичных объектов.

o    Евклидово расстояние – наиболее известная мера расстояния:

 

d_ij – расстояние между объектами i и j, а x_ik – значение к-ой переменной для i-го объекта.

o    Квадратичное евклидово расстояние – возведение евклидова расстояния в квадрат во избежания ивзлечения корня – d².

o    Манхеттенское расстояние (Хемминга) –

o    Метрика Минковского –

, r >= 1

o    Расстояние Махаланобиса (обобщенное расстояние) – используется в случае зависимости объектов

Σ – общая внутригрупповая ковариационная матрица, Xi и Xj – векторы значений переменных для объектов i и j соответственно.

 

Во все меры можно ввести вес, тогда такие меры называются взвешенными.

 

«-» Оценка сходства сильно зависит от различий сдвига в данных. Влияние переменных с большим средним и отклонением;

Можно пытаться провести стандартизацию, но тогда появляется опасность усилить «зашумленность» от плохо разделяющей переменной.

 

·          Коэффициенты ассоциативности (например, коэффициент Жаккара) – применяется для определения сходства между объектами, описываемыми бинарными переменными. Построение матрицы ассоциативности между двумя объектами:

   1 0

1 3 0

0 2 1

 

 

·          Вероятностные коэффициенты сходства – сходство между объектами не вычисляется. При образовании кластеров вычисляется информационный выигрыш от объединения двух объектов, а затем те объединения, которые дают минимальный выигрыш рассматриваются как один объект. Эта мера пригодна лишь для бинарных данных.

 

7.       Классификация методов кластер-анализа.

 

·          Иерархические агломеративные методы;

·          Иерархические дивизимные методы;

·          Итеративные методы группировки;

·          Методы поиска модальных значений плотности;

·          Факторные методы;

·          Методы сгущений;

·          Методы, использующие теорию графов.

 

8.       Иерархические агломеративные и дивизимные процедуры. Построение дендограммы. Формула рекуррентного пересчета расстояния между кластерами.

 

·          Иерархические агломеративные методы;

o    В начале каждый объект считается отдельным кластером. Задается матрица расстояний.

o    По матрице расстояний определяются два кластера, наиболее близкие друг к другу, они объединяются и образуют новый кластер.

o    Пересчитывается матрица расстояний. Размерность матрицы уменьшается за счет удаления двух строк и двух столбцов.

o    Шаги 2 и 3 повторяются до тех пор, пока не достигнуто необходимое число кластеров или заданная мера сходства (расстояния). Если условия не были заданы, то алгоритм останаливается, пока все объекты не будут объединены в один кластер.

·          Иерархические дивизимные методы;

o    Противоположность агломеративным методам

o    В начале все объекты принадлежат одному кластеру, а затем этот всеобъемлющий кластер разрезается на последовательно уменьшающиеся «ломтики».

§   Монотетический кластер – группа, все объекты которой имеют приблизительно одно и то же значение некоторого конкретного признака. Принадлежность к такому лкастеру определяется по фиксированным признакам.

§   Политетический кластер – группа, для принадлежности к которой достаточно наличия определенных сочетаний из некоторого подножества признаков.

o    Применяется в основном для бинарных данных.

 

·          Построение дендрограммы – графическое отображение результатов кластеризации, существенное преимущество всех иерархических алгоритмов. По горизонтальной оси откладываются номера объектов, по вертикали – мера расстояния, т.е. значения межклассовых расстояний, при которых произошло объединение классов.

·          Формула рекуррентного пересчета расстояния между кластерами:

o    Метод одиночной связи или ближайшего соседа – расстояние между классами определяется как расстояние между ближайшими членами классов.

«-» получение цепных, серпантинных кластеров

«+»применению метода не мешает наличие «совпадений» в данных.

o    Метод полной связи или дальнего соседа – расстояние между классами определяется как расстояние между самыми удаленными парами объектов. Метод создает компактные кластеры в виде гиперсфер.

o    Метод средней связи – расстояние между классами определяется как среднее значение исходных попарных расстояний между элементами, принадлежащими этим двум классам.

o    Метод медиан – расстояние между классами определяется как расстояние между точками с медиальными значениями всех показателей объектов, принадлежащих данным классам.

o    Метод центроид – расстояние между классами определяется как расстояние между центрами тяжести классов. Центр тяжести – это точка со средними значениями всех показателей с учетом весов отдельных элементов.

o    Метод Уорда – метод, оптимизирующий минимальную дисперсию внутри кластеров. Использует целевую функцию.

·          Недостатки:

o    Обработка и хранение большой матрицы сходства;

o    Распределение объектов по кластерам за один проход;

o    Изменение решения (иногда значительное) при изменении мартицы сходства.

 

9.       Иерархические дивизимные процедуры.  (см. выше)

 

10.    Итеративные методы кластер-анализа, основанные на понятии ядра. Параллельные и последовательные процедуры.

 

- итеартивные методы работают непосредственно с первичными данными.

- просматривают данные несколько раз в ходе алгоритма.

- не образуется иерархических кластеров.

- число кластеров должно быть известно заранее.

 

Параллельные процедуры – на классификацию поступают все объекты

o    Метод К-средних (K-means) –

ü  Исходное разбиение на k кластеров и вычисление центров тяжести (средних) этих кластеров;

ü  Просмотр всех наборов данных, помещение каждого объекта в кластер с ближайшим центром тяжести;

ü  Вычисление новых центров тяжести вновь образовванных кластеров;

ü  Шаг 2 и 3 повторяется до тех пор, пока не перестанут меняться кластеры.

o    Метод К-эталонов- идея алгоритма: совокупность объектов, находящихся на одинаковом расстоянии от каждого из k эталонов (ядер), образует компактную группу.

ü  Выбирается k эталонов и порог d;

ü  Объекут Оi ставится в соответствие код из k двоичных символов: «1» – если расстояние до k-го эталона меньше порогового, «0» - в противном случае.

ü  Выборка разбивается на кластеры, содержащие объекты с одинаковым кодом.

ü  Число эталонов необязательно должно быть равно числу кластеров

Последовательные процедуры – на классификацию объекты поступают по одному или малыми порциями.

Пример:

o    В основе алгоритма лежит предположение, что представители одного класса не могут быть удалены друг от друга более, чем на заданную пороговую величину;

o    На классификацию объекты поступают по одному;

o    1 шаг: Первый объект объявляется ядром е1 первого класса;

o    m-ый шаг: m-ый объект проверяем по следующему правилу:

ü  если расстояние от объекта до одного из ранее объявленных ядер меньше порогого, то добавляем к классу, данного ядра;

ü  если все ядра находятся дальше порогого значения, то объявляем новый класс и новое ядро.

Недостатки:

- проблема локального оптимума: применение процедуры проверки результата на достоверность;

- требование задавать число кластеров.

 

11.    Методы построения размытых кластеров. Нечеткий кластерный анализ

 

Причина возникновения:

ü  В классических методах кластерного анализа применяется так называемое двоичное (бинарное) разделение. Однако часто в реальных данных очень трудно построить четкие границы между классами. Из-за дискретного характера разбиения на классы данные классифицируются некорректно.

 

Нечеткие множества:

ü  Используя нечеткие множества, принадлежность выражается в виде вероятности от 0 до1.

 

Методы нечеткого кластерного анализа:

ü  Fuzzy C-means

o    Основан на методе k-средних (“Hard C-means”);

o    Во все формулы, включающие в себя элемент матрицы разбиения включается коэффициент нечеткости w (fuzzification factor) – от 1 (дискретный) до бесконечности (полностью размытые границы);

o    Обычно используется w=2.

o    Недостаток:

§   Поиск кластеров определенной формы:

·          Евклидово расстояние – гиперсферы;

·          Расстояние Хемминга – «бриллианты»;

·          Расстояние Чебышева – гиперкубы

§   Неоправданное огрубление результата.

ü  Кластеризация по Гюстафсону-Кесселю

o    Поиск кластеров в форме эллипсоидов;

o    Кластер характеризуется центроидом и ковариационной матрицей.

ü  Fuzzy C-varieties

o    Вместо того, чтобы выражать расстояние между двумя объектом и центроидом, мы можем представить, что центроиды – это более сложные геометрические конструкции, например, в методе Fuzzy c-Ellipsoids.

o    Кластер представляется в виде r-мерного множества и определяется центроидом и набором ортогональных векторов.

ü  Possibilistic Fuzzy C-means (P-FCM)

o    Определение объектов-выбросов (атипичных объектов);

o    В целевой функции используется взвешивающий коэффициент β, регулирующий суммарную принадлежность объектов к кластерам и выбросы образуют отдельный кластер.

ü  Noise Clustering

o    Выявление «шума» в данных;

o    Определение специального кластера (кластер «шума»), который позволяет локализовать и поместить «шум» в отдельный кластер;

o    В целевой функции используется взвешивающий коэффициент   , определяющий расстояние между «чистыми» данными и кластером «шума»;

o    Алгоритм заканчивает работу с c+1 кластерами.

ü  Достоинства:

o    Кластеризация становится более применимой к реальным данным;

o    Анализ граничных объектов и снижение их влияния на процесс кластеризации.

ü  Недостатки:

o    Допущение об определенной форме кластеров;

o    Алгоритмы строятся на расположении центроидов кластеров, а не совокупности точек в нём;

o    Невозможность обработки вложенных кластеров (например, вложенных сфер).

 

12.    Использование теории графов в кластер-анализе.

 

o    Алгоритм «Вроцлавская таксономия» - строится кратчайший незамкнутый путь (КНП): соединяются ребром две ближайшие точки, затем отыскивается точка, ближайшая к любой из уже рассмотренных точек, и соединяется с ней и т.д. до исчерпания всех точек. Такой способ повторяет метод ближнего соседа. В найденном КНП отбрасывают k-1 самых длинных дуг и получают k классов.

o    Алгоритм «Случайное разрезание графа сходства» - из полного графа сходства случайным образом производится выборка вершин, между которыми строится КНП. Запоминаются все его звенья и частоты их повторяемости. Звенья с частотами, большими n (задаваемый параметр), рассматриваются как межклассовые и отбрасываются. т.е. происходит разрезание графа. Процедура основана на том, что межклассовых расстояний всегда больше, чем внутриклассовых. Алгоритм является первой процедурой «случайной кластеризации», перспективной для больших массивов данных.

 

«+» возможность графического представления.

 

13.    Методы поиска модальных значений плотности.

 

Эти методы рассматривают кластер как область пространства с «высокой» плотностью точек по сравнению с окружающими областями. Они «обследуют» пространство в поисках скоплений данных, которые и представляют собой области высокой плотности

o    Методы, основанные на кластеризации по одиночной связи – препятствуют образованию цепочек. В методах поиска модальных значений плотности используется правило: отдавать предпочтение образованию нового кластера, а не присоединению объекта к существующему. Пример, модальный анализ.

«-» зависимость от выбора шкал;

«-» кластеры образуются сферической формы.

o    Методы разделения «смесей» многомерных вероятностных распределений – смесь – это совокупность выборок, представляющих различные совокупности объектов. Решается задача ращепления смеси: по выборке классифицируемых наблюдений построить статистические оценки для числа компонентов смеси k; построить статистические оценки их априорных вероятностей; для каждого из компонентов построить функции плотности. Данная постановка является наиболее полной. Часто, зная число компонент, нудно определить лишь функции плотности.

ü  Процедуры, работающие «от оценивания параметров смеси к классификации» - в начале находятся оценки неизвестных параметров, например, методом максимального правдоподобия.

Пример: ЕМ-алгоритмы – Название происходит от Estimation –оценка параметров, Maximization – максимизация функции правдоподобия.

Оценка происходит на основании допущений:

o    Классификация производится на основе смеси распределений;

o    Смесь состоит из известного числа классов k;

o    Распределение признаков в одном классе представлено одним распределением;

o    Априорные вероятности классов неизвестны.

Задача оценивания параметров смеси по выборке очень сложна. Одна из главных проблем – выбор числа классов анализируемой смеси k.

Сам алгоритм состоит в том, чтобы определить принадлежность объекта к классу, функция правдоподобия которого максимальна.

ü  Процедуры, работающие «от классификации к оцениванию» -

Пример: SEM-алгоритмы - Название происходит от Estimation –оценка параметров, Maximization – максимизация функции правдоподобия, Stochastique – статистическое моделирование.

Идея алгоритма состоит в том, что задача классификации начинается с разбиения совокупности классифицируемых наблюдений на k подвыборок, а затем для каждой подвыборки применяется оценка параметров, после чего уточняется разбиение.

«-» Эти методы основаны на статистической модели, и далеко не для всех задач смесь может быть разделена.

 

14.    Проверка качества разбиения совокупности данных на кластеры.

 

·       Визуальные средства оценки степени разнесенности и компактности выделенных групп объектов – отображение объектов в одно-, дву-, трехмерном пространстве с указанием их групповой принадлежности в виде гистограмм или диаграмм рассеивания. Также это могут быть графики средних.

·       Оценка качества классификации с помощью функционалов качества – проверяются неформальные требования к образованному разбиению: внутри группы объекты должны быть тесно связаны между собой; объекты различных групп должны быть далеки друг от друга; распределение объектов по кластерам должно быть равномерным.

o    Сумма квадратов расстояний до центров классов (внутриклассовый разброс)

 - вектор значений переменных для i-го объекта;

- центр тяжести l-ой группы;

n_l – число элементов l-ой группы;

 - расстояние между i-ым объектом и центром l-го кластера.

o    Сумма внутриклассовых расстояний между объектами

o    Суммарная внутриклассовая дисперсия

o    Объясненная доля общего разброса

§   Общее рассеивание

- общий центр тяжести l-ой группы;

§   Межклассовый разброс

 

§   T = 1 –SW/S, 0 <= T <= 1. Чем больше Т, тем больше доля общего разброса точек объясняется межклассовым разбросом, и можно считать, что тем лучше качество разбиения.

o    Коэффициент Дэвиса-Болдина;

o    Коэффициент RMSSTD.

·          Выявление среди полученных групп кластеров и сгущений – проводится анализ образованных групп на наличие в них кластеров и сгущений (чем больше их, тем лучше):

o    Кластером – называется группа объектов Gi такая, что выполняется неравенство

o    Сгущением – называется группа объектов Gi, если максимальный квадрат расстояния объектов из Gi  до центра группы меньше среднего квадрата до общего центра

·          Метод проверки на основе кофенетической корреляции – данный метод используется только для иерархических агломеративных методов. Конефетическая корреляция показывает, насколько хорошо сходство (или несходство) между объектами представляется дендрограммой, полученной с помощью агломеративных иерархических методов. Строится вторичная матрица сходства между всеми парами объектов, и корреляция между значениями исходной матрицы и вторичной матрицы – и есть конефетическая корреляция.

«-» содержание информации в этих двух матрицах различно.

·          Тесты значимости для признаков, используемых при создании кластеров – применение многомерного дисперсионного анализа признаков, для выяснения, является ли разбиение на кластеры значимым. Используется критерий Фишера.

·          Тесты значимости для внешних признаков – метод основан на применении многомерного дисперсионного анализа признаков, не участвующих в кластерном анализе.

«-» очень дорогостоящий.

·          Метод проверки, основанный на повторной выборке – метод основан на том, что к различным выборкам из одной и той же генеральной совокупности применяется одинаковый метод кластерного анализа. Однако данный метод не доказывает обоснованность решения, а только позволяет оценить степень устойчивости кластерного решения.

·          Методы Монте-Карло –

o    Для оценки результатов классификации: генерируется множество искусственных данных, которые не принадлежат исходной выборке, но обладают схожими характеристиками. Далее к каждому из наборов данных применяется один и тот же метод кластерного анализа, полученные результаты сравниваются с помощью тестов значимости, основанные на F-отношении. И делается вывод об обоснованности числа выделенных кластеров.

o    Для оценки самих методов кластеризации – генерируется выборка с заранее известным числом кластеров, и запускается метод кластеризации. Далее оценивается вероятность ошибки классификации, которая и определяет качество разбиения анализируемым методом.

 

15.    Локальные и глобальные правила остановки.

 

Критерии определения предпочтительного числа кластеров (только для иерархических методов):

·          Локальные – так как оценивает критерий остановки при k=1

o    Duda и Hart предложили критерий, основанный на следующем отношении:

где w[2] – сумма квадратов внутрикластерных расстояний в случае, когда данные распределены по двум кластерам;

w[1] – сумма квадратов внутрикластерных расстояний в случае одного кластера.

Гипотеза о существовании единого кластера данных отвергается, если значение критерия F₁ меньше, чем критическое значение:

n – число объектов для классификации,

р – число признаков,

z_1-α – квантиль стандартного нормального распределения уровня 1-α.

Тест отвечает на вопрос, есть ли вообще структура(кластеры) в данных или они однородны.

o    Beale предложил другую статистику:

где все обозначения смотри выше.

Данный критерий имеет распределение Фишера. Основная гипотеза состоит в постулировании одного кластера, и нет оснований её принять, если значение критерия больше критического уровня статистики.

Хотя данные критерии решают вопрос относительно двух кластеров, их можно применять не только на последнем шаге иерархического метода, но и на предыдущих.

«-» ограниченность сравнения и необходимость задания уровня значимости (постулируется возможность наличия ошибки)

 

·          Глобальный – Calinski и Harabasz предложили следующий критерий:

,

где B, W – матрица межкластерных и внутрикластерных сумм квадратов расстояний,

k –число кластеров.

Максимальное значение критерия указывает на наиболее вероятное число кластеров. При проведении иерархического кластерного анализа на каждом шаге определяется значение критерия и находится число кластеров k, при котором F₃ оптимально (максимально).

«-» правило не определено при k=1, то есть не исследуется оптимальность при отсутствии разбиения, а значит не решается вопрос – а должны ли вообще разбиваться данные.

 

16.    Дискриминантный анализ (ДА): основные понятия, допущения модели и их влияние на результат. Основные этапы.

 

Дискриминантный анализ – совокупность алгоритмов, порождающих на основании предположений и выборки конкретное правило классификации. Основным предположением ДА является то, что существует две или более групп, которые по некоторым переменным отличаются друг от друга.

В ходе анализа решается две задачи:

·          Интерпретация - описание аналитически или графически различий между объектами разных групп;

·          Разделение объектов по группам – построение правил классификации для новых объектов.

 

Дискриминантные переменные – характеристики, применяемые для того, чтобы отличить один класс от другого. Эти переменные должны измеряться либо по интервальной шкале, либо по шкале отношений.

 

Допущения классического ДА:

·          Должно быть два или более классов: g>=2;

·          По крайней мере два объекта в каждом классе: n_i>=2;

·          Любое число дискриминатных переменных при условии, что оно не превосходит общее число объектов минус 2: 0 < p < (n-2);

·          Ни одна переменная не может быть линейной комбинацией других переменных, отсюда следует линейная независимость ДП;

·          Ковариационные матрицы для генеральных совокупностей равны между собой для различных классов;

·          Закон распределения дискриминатных переменных для каждого класса является многомерным нормальным, т.е. каждая переменная имеет нормальное распределение при фиксированных остальных переменных.

 

Эти допущеня фундаментальны для ДА. Если экспериментальные данные для некоторой конкретной задачи не вполне удовлетворяют этим предположениям, то статистические выводы не будут точным отражением реальности и следует дополнительно решать вопрос о целесообразности этих процедур.

 

17.    Построение канонических дискриминантных функций. Интерпретация коэффициентов.

 

Каноническая дискриминантная функция – линейная комбинация ДП и удовлетворяющая определнным условиям.

fkm – значение канонической дискриминатной функции для m-го объекта в k-ой группе;

Xikm – значение i-й ДП у m-го объекта в группе k;

ui  - коэффициенты, обеспечивающие выполнение требуемых условий.

 

Коэффициенты u  для первой функции выбираются таким образом, чтобы её средние значения для различных классов как можно больше отличались друг от друга. Коэффициенты для второй функции выбираются также, но с дополнительным условием: значения второй функции не должны коррелировать с первой и т.д. Максимальное число КДФ равно числу классов минус один, или числу ДП. В зависимости от того, какая из этих величин меньше.

 

Основные принципы получения коэффициентов u -  для этого необходимо ввести статистический критерий для измерения степени различий между объектами. Вводятся три матрицы:

·          Матрица Т общегруппого разброса

 - среднее значение переменной по всем классам.

Если разделить каждый элемент матрицы на (n-1), получим ковариационную матрицу. Далее если разделить каждый элемент  на квадратный корень двух соответствующих диагональных элементов, то получим корреляционную матрицу. Но в ДА чаще применяют матрицу Т.

 

·          Матрица W внутригруппового разброса – отличается от Т тем, что её элементы определяются средними значениями переменных для отдельных классов, а не общими средними.

Также можно получить ковариационные и корреляционные матрицы для групп.

·          Матрица В межгруппового разброса: B = T – W.

 

Один из методов поиска наилучшей дискриминации данных заключается в нахождении такой КДФ, которая бы максимизировала отношение межгруппого разброса к внутригрупповому

                       

Далее решается система уравнений:

 

λ – собственное число

ν_{i –} последовательность р коэффициентов ДФ.

Известны только b, w. Находят собственное значение и v. Далее находим коэффициенты ДФ:

Нормировка деляется для того, чтобы оси брали начало координат от главного центроида. (?)

 

Интерпретация КДФ:

Подставляя ДП в КДФ, мы получаем координаты объекта в пространстве КДФ, и сможем сравнивать насколько далеки или близки объекты по отношению друг к другу.

Можно отобразить объекты из выборки на графиках для визуального анализа, но в случае большого количества КДФ это становится сложно.

 

18.    Проверка значимости дискриминантных функций. Остаточная дискриминантная способность.

 

Для проверки значимости КДФ существуют следующие подходы:

·          Собственное значение λ – чем больше это значение, тем больше групп будет разделять соответствующая функция.

·          Относительное процентное содержание – собственное значение делится на общую сумму. Этот показатель показывает насколько функция слабее по сравнению с другими.

·          Коэффициент канонической корреляции – мера связи между группами и КДФ. Нулевое значение – отсутствие связи, большее значение – сильная связь. Каноническая корреляция отражает реальную полезность КДФ.

·          Остаточная дискриминантная способность – способность переменных различать классы, если исключить информацию с помощью ранее вычисленных функций. Если эта величина мала, то дальше нет смысла искать КДФ. Для получения ОСП используют Λ-статистику Уилкса – мера различий между классами по нескольким переменным. Чем она ближе к нулю, тем выше различение, чем ближе к 1, тем хуже различимость.

·          Тест значимости χ² – на основе статистики Уилкса получим значение статистики χ^2..

 

19.    Построение правила классификации. Использование классифицирующих функций в ДА. Матрица классификации.

 

Фишер предложил применять для классификации линейную комбинацию ДП, которая максимизирует различия между классами, но минимизирует дисперсию внутри классов:

h_k  - значение функции для класса k;

b_ki – коэффициенты, которые необходимо определить.

Объект относят к тому классу, для которого получится наибольшее значение функции. Коэффициенты классифицирующих функций обычно не интерпретируются, и точное значение функций такж не важно, главное различимость значений для разных классов.

Такие функции называют простыми классифицирующими функциями.

 

Правила тестируются на тестовой выборке и строится матрица классификации – таблица, строки соответствуют исходным группам, а столбцы – полученным после классификации.

 

20.    Построение правила классификации на основе расстояния Махаланобиса и апостериорной вероятности.

 

Обобщенные функции расстояния и вероятность принадлежности к классу:

Махаланобиса предложил обобщенную меру расстояния, а именно квадрат расстояния от точки Х до центроида данного класса Gk.

После вычисления расстояния до каждого класса объект относится в группу наименьшим D². Предполагается равкнство ковариационных матриц классов.

 

Вероятность принадлежности к классу:

Относя объект к ближайшему классу, мы неявно приписываем его к тому классу, для которого он имеет наибольшую вероятность принадлежности. Для любого объекта сумма этих вероятностей по всем классам не обязатетельно равна 1. Однако можно сделать предположение о том, что объект должен принадлежать одной из групп, тогда можно вычислить апостериорную вероятность принадлежности для любой из групп.

 

21.    Процедуры отбора оптимального состава дискриминантных переменных.

 

Пошаговый дискриминантный анализ применяется для выбора хороших дискриминаторов из ДП, а также для ранжирования ДП по степени их полезности. Наиболее широко используемый метод отбора переменных основан на следующем критерии отбора – на отношении внутренней обобщенной дисперсии к общей обобщенной дисперсии для отбираемых переменных. Применяется Λ-статистика Уилкса:

Значение, близкое к 1, указывает на то слабое разделение между группами, в то время как малое значение на хорошее разделение между группами.

Для оценки значимости изменения  Λ в результате добавления переменной применяют статистику Фишера F.

Существует два вида последовательного отбора:

·          F-статистика включения – оценивает улучшение различения от использования рассматриваемой переменной по сравнению с различением достигнутым с помощью других уже отобранных. Стастика проверяется на значимость – так как не должна быть мала;

·          F-статистика исключения – оценивает значимость ухудшения различения после удаления переменных из списка уже отобранных. Часто эта процедура проводится с целью ранжирования переменных, так как она удаляет шаг за шагом почти все переменные из модели.

Также вводится понятие толерантности – толерантность для включения ДП равна единице за вычетом квадрата её внутригрупповой корреляции с текущими включенными переменными. Если проверяемая переменная является линейной комбинацией одной или нескольких отобранных ранее переменных, то её толерантность или равна, или близка к нулю. В качестве критерия используют расстояние Махаланобиса.

 

22.    Снижение размерности данных. Постановка задачи и методы решения.

 

Снижение размерности обусловлено:

·          Наглядное представление (визуализация) – проецирование в трех-, двухмерное пространство;

·          Лаконизм исследуемых моделей – связано с необходимостью  упрощения счета и интерпретации полученных статистических результатов;

·          Сжатие объемов хранимой статистической информации – без видимых потерь в информативности сжатие хранимых данных в матрицах.

·          Устранение дублирования информации и незначимых признаков.

 

Задача заключается в определении такого набора признаков P, найденного в классе F допустимых преобразований исходных данных показателей, что

Методы:

·          Метод главных компонент – в процессе вычисления получают все главные компоненты и их число первоначально равно числу исходных признаков; постулируется возможность полного объяснения дисперсии через полученные компоненты.

·          Методы факторного анализа – дисперсия признаков здесь не объясняется в полном объеме, признается, что часть дисперсии остается нераспознанной как характерность. Процесс выделения факторов последователен и может быть прерван на любом шаге, если принято решение о достаточности дисперсии исходных признаков.

 

23.    Модели и методы факторного анализа.

 

·          Модель классического факторного анализа – требует наилучшее воспроизведение корреляции;

·          Модель главных компонент – требует максимально возможный суммарный вклад в дисперсию;

·          Модель современного факторного анализа – совокупность методов, выявляющих скрытые характеристики в данных.

 

Общая цель – определение факторных нагрузок.

 

24.    Метод главных компонент.

 

Модель его проста:

  i=1…n

где каждый из наблюдаемых признаков линейно зависит от r некоррелированных между собой новых комопонент p. Каждая очередная компонентая дает макисмально возможный вклад в суммарную дисперсию параметров.

 

25.    Фундаментальная теоpема в случае коppелиpуемых и некоррелируемых фактоpов.

 

Л.Тэрстоуном равенства R = ACA^T  и R = ACA^T названы фундаментальной теоремой факторного анализа. С – является матрицей коэффициентов корреляции между факторами. Если постулируются ортогональные факторы, то С становится единичной матрицей.

Фундаментальная теорема утверждает, что корреляционная матрица  R  может быть воспроизведена с помощью факторного отображения А и корреляции между факторами.

 

26.    Классификация факторов и связи между отдельными видами факторов.

 

·          Генеральный – все его нагрузки значительно отличны от 0 (больше 0,6).

·          Общий – хотя бы две его нагрузки значительно отличны от 0. Генеральный фактор А является частным случаем общего фактора.

·          Характерный – только одна нагрузка значимо отличается от 0.

 

27.    Составляющие полной дисперсии переменной (общность, хаpактеpность, спецефичность, надежность).

 

 

h_i² -  - сумма квадратов нагрузок общих факторов или общность – та часть полной (единичной) дисперсии, которую можно приписать общим факторам.

u_i² – 1 - h_i² – доля дисперсии, которая соответствует квадрату нагрузки определенного фактора u_i² и называется характерностью, т.е. та часть дисперсии, которая не связана с общими факторами.

Характерность делится на:

·          Специфичность  - та доля единичной дисперсии, которая не связана с общими факторами и присуща лишь одной определенной переменной.

·           - дисперсия, обусловленная ошибкой.

 

       Надежность – специфичность + общность.

 

28.    Схема решения и основные проблемы факторного анализа.

 

Схема факторного анализа:

 

 

Проблемы:

·          1 Общности – получение значения оценок общностей, которые проставляются по главной диагонали корреляционной матрицы R и получается редуцированная матрица R_h.

·          2 Факторов – извлечение факторов из R_h и получение матрицы А.

·          3 Вращения – выбор одной из большого числа матриц А, которые одинаково хорошо воспроизводять R_h=АА^Т

·          4 Оценка факторов – оценка значения факторов для каждого индивидуума.

 

29.    Геометрическая интерпретация модели факторного анализа.

 

Целью факторного анализа является снижение размерности данных за счёт создания новых характеристик объектов на основе исходных. В геометрическом смысле объекты являются точками в многомерном пространстве исходных характеристик. В геометрическом смысле, целью факторного анализа, является поиск проекций этих объектов в другие пространства. Причем такие пространства, в которых количество осей будет меньше чем в исходном пространстве при минимальной потере информации о различиях (Тоесть не значимые потери о различиях).

 

30.    Пространство общих факторов и полное фактоpное пpостpанство.

 

Пространство общих факторов - пространство наименьшей размерности в котором можно представить m переменных в виде векторов. Любое другое пространство с меньшей размерностью не смогло бы включить в себя все переменные. Любое пронстранство большей размерности, обладало бы большими, чем это необходимо возможностями. Размерность ПОФ соответствует рангу матрицы исходных данных или ранку корреляционной матрицы.

В геометрической интерпретации в пространстве общих факторов координатные оси являются факторами, а вектора  представляют переменные. Координатные оси стандартизованы и равняются 1, т.к. дисперсия фактора должна равнятся еддинице.

 

Пример

Пространство общих факторов для матрицы A= имеет вид

Длина вектора, представляющего переменную в общем факторном пространстве равна корню из общности.

 

Наибольшая возможная длина равна 1. При геометрической интерпретации длина вектора укащывает на то, какая доля единичной дисперсии каждой переменной является общей с факторами.

 

Полное фактоpное пpостpанство. Данное пространство образовано столбцами матрицы F (содержит нагрузки общих и характерных факторов), представляющих координатные оси в этом пространстве. Т.к данное пространство натянуто как на общие, так и на характерные факторы, то пространство общих факторов является подпространством полного факторного пространства. Длину вектора в полном факторном пространстве можно выразить: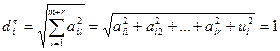

 

 

31.    Проблема факторов. Выделение факторов с помощью метода главных компонент. Другие методы решения.

 

Проблема факторов состоит в установлении числа и вида осей координат, необходимых для отображения корреляции m переменных. Существует несколько вариантов решения данной проблемы: A. многофакторные решения: метод главных факторов, центроидный метод. B. метод выделения факторов (однофакторный, бифакторный и т.д.). C. новые методы решения, основанные на статистических подходах (метод максимального правдоподобия, альфа-факторный анализ).

При любых способах решения этой задачи, вводятся ограничения, чтобы однозначно определить систему равенств: . У каждого метода есть свои ограничения, введение кот. позволяет получить однозначное решение. В большинстве случаев. исп. методы первой группы.

 

При решении задачи измерения трех нормально распределенных параметров у n индивидуумов, получается ситуация (рис.1), где n точек сосредоточены в трехмерном пространстве с тремя осями переменными X,Y,Z в облаке вокруг общего центра тяжести. Это облако точек наблюдений в общем случае имеет овальную форму и называется эллипсоидом. В частном случае, когда во всех трех направлениях дисперсия одинакова по величине, получают шар.

На рис. изображено овальное тело с тремя секущими плоскостями (различно заштрихованными), проходящими через центр тяжести. Оси координат исходных, переменных X, Y, Z являются более или менее произвольными. Очевидно, что имеется бесконечно много систем координат, в которых можно изобразить наблюдаемые точки. Одна из них представляет интерес. Это система координат главных осей:  • первой главной осью λ₁ является самый длинный диаметр овального тела; • второй главной осью λ₂ является самый длинный диаметр в плоскости, ортогональной к первой главной оси и проходящей через центр тяжести системы (заштрихована вертикально); • третья главная ось λ₃ в трехмерном случае перпендикулярна к первой и второй главным осям и проходит через центр тяжести.

В геометрическом плане метод главных факторов состоит в том, что: • определяют самую длинную ось эллипсоида Она является первой главной осью, которая должна пройти через центр тяжести, на рис.1 эта ось обозначена буквой λ₁. • устанавливают подпространство - в данном случае плоскость, - которое перпендикулярно к первой главной оси и которое проходит через центр тяжести (на рис.1 заштриховано вертикально). В этом подпространстве находится следующая по величине ось скопления точек и т. д., пока не будут определены последовательно все главные оси.

Длины главных осей пропорциональны величинам дисперсий в направлении соответствующей главной оси. С помощью метода главных факторов устанавливаются направления этих осей относительно первоначальной системы координат. Главные оси соответствуют факторам, которые должны быть лишь надлежащим образом пронормированы, чтобы выполнялось требование единичной дисперсии факторов.

Переход от системы координат XYZ к системе λ₁λ₂λ₃ соответствует геометрическому решению задачи выделения факторов, осуществляемому с помощью метода главных факторов. Этот переход от одной системы координат к другой без потери информации на практике большей частью возможен лишь тогда, когда определяются все главные компоненты, т. е. для m переменных определяют m главных компонент.

Алгебраическое решение. Классическая модель . Предположим, что , и считаем  известной и для вывода приравниваем к 0. Необходимо реш. систему уравнений: . Условия для реш. системы уравнений:

- сумма квадратов нагрузок первого фактора должна составлять максимум от полной дисперсии: ;

- сумма квадратов нагрузок второго фактора должна составлять максимум оставшейся дисперсии т т.д.

Необходимым и достаточным условием существования нетривиального решения этой системы является равенство 0 детерминанта матрицы коэффициентов этих уравнений.

 

 

32.    Критерии оценки числа факторов, подлежащих выделению.

 

1) Анализ долей дисперсий 1.Выделяется такое кол-во факторов, на которое в сумме приходится 90% полной дисперсии.(на рис. – 3 фактора) 2. Выделить только те факторы, дисперсия каждого из которых составляет более 5% полной дисперсии (на рис. – 4 фактора). Критерий Кайзера-Дикмана: факторы, вклады которых в полную дисперсию (сумма квадратов факторных нагрузок; собственное значение) меньше 1 не должны выделяться

 

 

 

 

 

 

2)Анализ собственных значений. Критерий отсеивания(Каттела). Анализируется графическое изображение всех собственных значений корреляционной матрицы, которые наносятся в порядке убывания. Если правую часть кривой, на которой раполагаются точки, можно выровнять по прямой, то выделяются все факторы, которые не лежат на прямой + первый на прямой.(на рис. – выделяется 5 факторов)

 

 

 

 

 

 

3)Оценка остатков корреляций. Если все остаточные коэф-ты в матрице остатков незначимо отличаются от 0, то нет смысла в выделении нового фактора

 

Факторов должно быть меньше, чем исх. переменных минимум в 2 раза.

 

 

33.    Пpоблема общности. В чем она состоит и как pешается.

 

По определению, общность h_i²_,  переменной i = сумме квадратов нагрузок общих факторов. Т.к. Дисперсия каждой i-й пере­менной приводится к 1, общность является долей единичной дисперсии, которая обуславливается оющими для нескольких переменных факторами. Отсюда вытекает необходимость подбора значений общностей меньше 1. Общности могут принимать значения 0..1. Есть много методов оценки h_i². При большом числе переменных при неточные оценки общностей большей частью не оказывают сильного влияния на финальное факторное решение. 1.Способ наибольшей корреляции. Заключается в выборе наибольшего коэффициента корреляции данной переменной с остальными. Этот метод лучше использовать при большом числе переменных m (>10), но он теоретически не обоснован. 2. Использование квадрата коэффициентов множественной корреляции.

R_i*12..i..m²-является нижней границей  h_i². Это наиболее распространённый метод. 3. Итеративная процедура (ЛР3?). Принимается решение об определении числа факторов r с помощью одного из методов.

 

34.    Проблема вращения и понятие наипростейшей факторной структуры.

 

Цель вращения: найти в пространстве общих факторов одну из возможных конфигураций легко интерпретируемых факторов. Конфи¬гурация - это система векторов, соотношения между которыми остаются постоянными.

Существует три различных подхода к проблеме вращения:

1)Графический. Вращение заключается в проведении новых осей. которые соответствуют некоторому критерию простой, легко интерпретируемой структуры. Если в пространстве факторов есть явные скопления точек, легко отделяемые друг от друга, простая структура получается в та» случае, когда оси проведены через эти скопления. Но если такое разделение не очевидно или число факторов велико, графический метод неприменим.

2)Аналитические методы. В этом случае выбирается некоторый объективный критерий, которым надо руководствоваться при выполнении вращения. В рамках этого подхода различают два вида вращения -ортогональное и косоугольное. Они в свою очередь имеют многочис¬ленные варианты.

3)Состоит в задании априорной целевой матрицы. Цель вращения -нахождение факторного отображения, наиболее близкого к некоторой заданной матрице. Целью всех вращений является получение наиболее простой фак¬торной структуры. К сожалению, концепция простоты неоднозначна, и поэтому не существует единых формальных критериев.

Факторная структура называется наипростейшей, когда все пере¬менные имеют факторную сложность не больше 1, т. е. когда каждая переменная имеет ненулевую (значимую) нагрузку только на один общий фактор. Для реальных данных такая структура недостижима. Следова-тельно, задача состоит в определении фактической структуры, которая является самой «близкой» к простой.

 

35.    Цель и конечный pезультат оpтогонального вpащения.

 

Фергюсон подошел к проблеме вращения с позиции наибольшей простоты или экономии при описании переменных в пространстве общих факторов. Он исходил из того, что самое экономное описание точки в двумерном пространстве соответствует такому ее положению, когда одна из осей проходит через нее. Следовательно, для наиболее экономичного описания точек нужно при вращении осей стремится к этому идеально­му случаю. Если одна из осей приближается к точке, то произведение двух ее координат начинает уменьшаться. Рассуждая так, он пришел к выводу, что в качестве меры экономии может служить сумма произведений координат множества точек

Но т.к. точки может иметь координаты + и -, то надо возвести в квадрат. Он будет стремиться к минимуму, кода наибольшее кол-во точек будет лежать вблизи оси.

Метод квартимакс, варимакс и модифицированный варимакс-критерий.

 

36.    Методы и критерии в ортогональном вращении.

 

Самое экономное описание точки в 2-мерном пространстве, когда одна из осей проходит через неё. Вывод, что в качестве меры экономии может служить сумма произведений координат множества точек. Но т.к. точки может иметь координаты + и -, то надо возвести в квадрат. Он будет стремиться к минимуму, кода наибольшее кол-во точек будет лежать вблизи оси. Метод квартимакс не нашёл широкого применения т.к. у него сильная тенденция к выделению генерального фактора. В настоящее время популярна его модификация варимакс. В этом методе было решено упростить каждый фактор (брать также и столбцы матрицы). В этом случае нагрузки близки к 1 либо 0, т.е. описываются более просто.  

Модифицированный варимакс-критерий:

 

 

37.    Цель и конечный pезультат косоугольного вpащения. Первичное и вторичное факторное решение. Критерии и методы, применяемые в косоугольном вращении.

 

Косоугольное вращение более общее, чем ортогональное, так как здесь нет ограничений, связанных с некоррелируемостью факторов. Преимущество его в следующем: когда в результате его выполнения получаются ортогональные факторы, можно быть уверенным, что эта ортогональность действительно им свойственна, а не внесена моментом вращения.

Метод квартимин основан на введении вторичных осей: если существуют разделимые скопления точек, определяемые первичны­ми факторами, то они будут иметь нулевые проекции на все вторичные оси, за исключением одной: , где  проекции i-го параметра на j-ю и k-ю вторичные оси. Величина будет 0, если все параметры имеют нагрузку только на один фактор. Цель вращения-нахождение таких нагрузок, которые минимизируют N.

Метод коваримин (covarimin) минимизирует ковариацию квадратов проекций на вторичные оси.

.

Прямой метод облимин. Основан на упрощении матрицы нагрузок первичных факторов (без использования вторичных осей). Используется тот же самый критерий, но вместо Vij - элементов факторной структуры -используются элементы матрицы первичного факторного отображения – bij. .

Как мы видим, возможно, представление косоугольного вращензя аналитически, однако в универсальных статистических пакетах пред­ставлены, как правило, только методы ортогонального вращения.

 

 

38.    Измерение факторов.

 

Конечный результат ФА-получение системы содержательно интерпретируемых факторов, воспроизводящих матрицу корреляции(R), однако можно ещё сделать и измерение факторов по значениям наблюдаемых переменных, т.е. представить исходные данные в виде значений полученных факторов (со снижением размерности). Этап часто называют факторным шкалированием. Это процедура, позволяющая присваивать каждому объекту некоторые числовые оценки значений выделенных факторов, используя значения наблюдаемых переменных для этого объекта. Набор из m признаков можно анализировать либо в терминах только общих и характерных факторов(модель компонентного анализа), либо в терминах совокупности только общих факторов(модель ФА). Основная модель ФА: Z=A*P (Z-матрица значений параметров(mxn), A-матрица факторных нагрузок(mxr), P-матрица значений факторов для объекта(rxn)). Можно преобразовать это выражение для более удобных вычислений P=M^-1*A^T*Z. Также, одна из задач этого этапа-содержательная интерпретация факторов, если мы доверяем полученной факторной структуре, то можно попытаться произвести осмысление природы каждого фактора, путём анализа общих черт переменных, имеющих высокие нагрузки на 1 фактор. 

 

39.    Программное обеспечение, используемое для интеллектуального анализа данных.

 

StatSoftStatistica

Описательные статистики и графики. Группировка. Корреляции Диаграмма рассеивания, матричная диаграмма рассеивания, анализ по группам. Интерактивный вероятностный калькулятор. T-критерии (и другие критерии групповых различий).

SPSS

Методы анализа данных:Описание данных, Прогнозирование числовых результатов, Сегментация/снижение размерности, Классификация, Инструменты анализа временных рядов.

Clementine-это автоматизированное рабочее место для data mining, позволяющее быстро разрабатывать прогностические модели с привлечением бизнес-экспертизы, а затем внедрять полученные модели для усовершенствования процесса принятия решений.

SAS EnterpriseMiner

Программный продукт Enterprise Miner – это интегрированный компонент системы SAS, созданный для выявления в огромных массивах данных информации, необходимой для принятия решений.

40.    Методы визуализации многомерных  данных.

 

•       3М XYZ графики:

–      Отклонения - данные интерпретируются как координаты X, Y, Z и отображаются в трехмерном пространстве в виде "отклонений" от заданного уровня на оси Z.

–      Пространств. - представление данных 3М диаграммы рассеяния при помощи плоскости XY, расположенной на выбранном пользователем уровне вертикальной оси Z (которая проходит через центр плоскости).

–      Спектральные - на таких диаграммах в плоскости горизонтальных осей можно строить зависимость частот спектра от последовательных временных промежутков, а на оси Z отмечать спектральные плотности на каждом интервале.

–      Трассировочные - точки данных располагаются так же, как и на обычных 3М диаграммах рассеяния (значения переменных соответствуют координатам X, Y и Z каждой точки), но при этом соединяются линией (в порядке их следования в файле данных), визуализируя "след" последовательных значений (например, движения, изменения параметров с течением времени и т.п.).

•       3М последовательные графики

–      Дискретные карты линий уровня - 2М проекциия 3М ленточной диаграммы. Каждая точка данных здесь представлена прямоугольной областью; значениям (или диапазонам значений точек данных) соответствуют различные цвета и/или шаблоны областей (диапазоны указаны в условных обозначениях). Значения внутри каждой серии откладываются по оси X, а сами серии - по оси Y.

–      Поверхность по исх. данным - подогнанная к каждой точке данных сглаженная сплайнами поверхность. Последовательные значения каждой серии откладываются по оси X, а сами последовательные серии представлены вдоль оси Y.

•       4М/Тернарные графики

–        Диагр.рассеяния - для представления трех (или более) переменных [компонент X, Y и Z] на плоскости используется треугольная система координат. Точки графика соответствуют пропорциям переменных-компонент (X, Y и Z).

–        Карты зон - проекция поверхности в виде зонной карты (подогнанной к множеству данных с четырьмя координатами).

–        Карты линий - проекция поверхности в виде карты линий (подогнанной к множеству данных с четырьмя координатами).

•       n-мерные пиктографики

–        Лица Чернова - для каждого наблюдения рисуется отдельное "лицо", где относительные значения выбранных переменных представлены как формы и размеры отдельных черт лица (например, длина носа, угол между бровями, ширина лица).

–        Столбцы - для каждого наблюдения рисуется своя столбчатая диаграмма; относительные значения выбранных переменных для каждого наблюдения выражаются высотами соответствующих столбцов.

–        Линии - для каждого наблюдения рисуется свой линейный график; относительные значения выбранных переменных для каждого наблюдения выражаются высотами соответствующих точек излома над уровнем линии основания.

–        Круг. диагр. - значения для каждого наблюдения представлены в виде круговых секторов (по часовой стрелке, начиная с 12:00); относительные значения выбранных переменных соответствуют площадям круговых секторов.

–        Многоугольн. - для каждого наблюдения рисуется свой многоугольник; относительные значения выбранных переменных выражаются расстояниями от центра пиктограммы до соответствующих углов многоугольника (по часовой стрелке, начиная с 12:00).

–        Профили - для каждого наблюдения рисуется своя область; относительные значения выбранных переменных для каждого наблюдения выражаются высотами соответствующих вершин контура над уровнем линии основания.

–        Звезды - для каждого наблюдения рисуется своя пиктограмма в виде звезды; относительные значения выбранных переменных выражены относительными длинами отдельных лучей каждой звезды (по часовой стрелке, начиная с 12:00). Концы лучей соединены линиями

–        Лучи - для каждого наблюдения рисуется своя пиктограмма в виде солнца; каждый луч отображает одну из выбранных переменных (по часовой стрелке, начиная с 12:00), а длина луча равна относительному значению соответствующей переменной. Значения переменных для каждого наблюдения соединены линией.

•       интервальные графики

–      Японские свечи - данный метод предсказать поведение рынка в будущем оказался наиболее интересным, поскольку в одном элементе он отбражал сразу четыре показателя вместо одного. Японцы быстро обнаружили, что на основании графиков построенных при помощи «свечей» можно с достаточной степенью вероятности предсказывать будущий спрос и поведение цены.

 

41.    Text Mining.

 

Технология глубинного анализа текста - Text Mining - это тот самый инструментарий, который позволяет анализировать большие объемы информации в поисках тенденций, шаблонов и взаимосвязей, способных помочь в принятии стратегических решений. Кроме того, Text Mining - это новый вид поиска, который в отличие традиционных подходов не только находит списки документов, формально релевантных запросам, но и помогает ответить на вопрос: "Помоги мне понять смысл, разобраться с этой проблематикой".

Технология эффективного анализа текста Text Mining преподает лишь наиболее ключевую и значущую информацию. Таким образом, пользователю незачем самому "просеивать" огромное количество неструктурированной информации. Разработанные на основе статистического и лингвистического анализа, а также искусственного интеллекта, технологии Text Mining как раз и предназначены для проведения смыслового анализа, обеспечения навигации и поиска в неструктурированных текстах. Применяя построенные на их основе системы, пользователи смогут получить новую ценную информацию - знания.

                Так сложилось, что наиболее часто встречается в Text Mining задача - это классификация - отнесение объектов базы данных к заранее определенным категориям. Фактически задача классификации - это классическая задача распознавания, где по обучающей выборке система относит новый объект к той или иной категории.

Вторая задача - кластеризация - выделение компактных подгрупп объектов с близкими свойствами. Система должна самостоятельно найти признаки и разделить объекты по подгруппам.

А так же анализ связей, которые определяют появление дескрипторов (ключевых фраз) в документе для обеспеченияи навигации.

И извлечение фактов - которое предназначено для получения некоторых фактов из текста с целью улучшения классификации, поиска и кластеризации.

Можно назвать еще несколько задач технологии Text Mining, например, прогнозирование, которое состоит в том, чтобы предсказать по значениям одних признаков объекта значения остальных.

Еще одна задача - нахождение исключений, то есть поиск объектов, которые своими характеристиками сильно выделяются из общей массы. Для этого сначала выясняются средние параметры объектов, а потом исследуются те объекты, параметры которых наиболее сильно отличаются от средних значений.

Несколько отдельно от задачи кластеризации стоит задача поиска связанных признаков (полей, понятий) отдельных документов. От предсказания эта задача отличается тем, что заранее не известно, по каким именно признакам реализуется взаимосвязь; цель именно в том и состоит, чтобы найти связи признаков. Эта задача сходня с кластеризацией, но не по множеству документов, а по множеству присущих им признаков.

И наконец, для обработки и интерпретации результатов Text Mining большое значение имеет визуализация.

 

42.    Web Mining

 

Цель: извлечение полезной информации из Интернет.

Классификация:

 

1.        Web Usage Mining – выявление шаблонов «поведения пользователей» (доступ к страницам, переходы навигация) путем анализа логов. Server logs and OLAP.

2.        Web Structure Mining – получение полезных знаний путем анализа структуры гиперссылок. PageRank, SpyLog.

3.        Web Content Mining – добыча, извлечение и интеграция полезных данных, информации и знаний из содержимого www-страницы. Поиск информации и извлечение информации.